[ML] 분류분석 - 이진분석

■ 분류분석 (Classification Analysis)

 

□ 정의 및 용도

- 종속변수가 범주형인 데이터에 대해 데이터의 유사성(특이성이 비슷한)이 높은 것들을 같은 종류로 분류

- 종속변수가 미리 결정된 범주 중 하나에 속할 가능성 또는 확률 예측 (분석 결과는 확률분포로 나옴)

- 미래 데이터 세트에서 동일한 패턴(유사한 시퀀스, 단어 또는 감정)을 찾고자 할 때 사용

 

□ 종류

1. 로지스틱 회귀분석

  : 종속변수가 범주형 변수일 때 사용, 시그모이드 함수 사용, 이진 분류시 가장 많이 사용됨  

 

2. 의사결정 트리

  : 나무형태의 그래프로 의사결정을 질문에 대한 Yes or No로 분기하여 데이터를 분류, 의사결정 과정을 도식화하고 시각화할 수 있는 방식임. (보통 딥러닝은 내부 의사결정구조가 매우 복잡해 시각화하기 매우 힘듦)

 

3.  나이브 베이즈

  : 조건부 방식으로, 데이터 집합의 예측 변수가 독립적이라고 가정하는 분류 알고리즘 

 

4. K-Nearest Neighbors

  : 데이터 포인트 간의 거리를 기반으로 데이터를 분류 및 예측하는 알고리즘

 

---

■  로지스틱 회귀분석 (Logistic Regression)

- 종속변수가 범주형일 때 입력변수를 기반으로 결과를 예측하기 위한 분석 방법

- 회귀식을 이용하여 새로운 값에 대한 분류를 하지만 목표변수가 범주형 변수인 경우에 사용한다는 점에서 일반 회귀분석과 차이가 있음.

- 이진분류 문제를 풀기위한 대표적인 알고리즘 (다중분류 문제도 가능하지만, 다중 분류를 이진분류로 치환해서 해결함)  

 

 

 

 

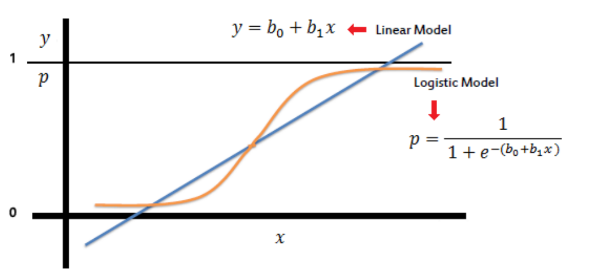
보통 회귀분석은 직선의 방정식임. 그런데 선형 방정식일 경우, 새로운 큰 값이 들어올수록 분류를 위해  직선의 기울기를 바꿔야 하는데 그렇게 되면 기존에 분류되었던 값들에도 영향을 미치고, 새로운 기준으로 재분류되기 때문에 이진분류 문제를 해결하기 위해서 비선형함수를 사용해야 함.

 

▶ 로지스틱 회귀분석

 

- 비선형 모델

- 지수함수를 활용한 회귀분석

- 확률밀도함수(출력 결과: 0~1) => 시그모이드 함수

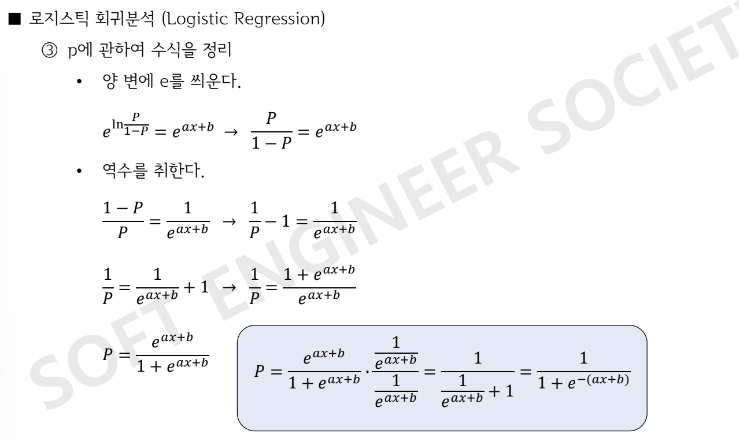
- 독립변수의 범위는 [-inf, inf]이고, 종속변수의 범위는 [0,1]임. 종속 변수의 범위를 무한대로 변환하기 위해 오즈(odds)와 logit function(오즈에 로그함수를 취하는 변환함수)를 활용함

 

 

 

※ 오즈 (odds) : 0 <= 오즈(= 성공확률/(1-성공확률)) <= inf

 : 성공확률이 0.75이면, 성공의 오즈는 0.75/0.25=3과 같음. 즉, 오즈가 3이면 성공 확률이 실패 확률의 3배임

 

 

 

 

 

▶ 로지스틱 회귀의 비용함수

 

- 크로스 엔트로피 함수 (CEE)

: 엔트로피는 불확실성의 척도로 정보이론에서의 엔트로피는 불확실성을 나타내며 엔트로피가 높다는 것은 정보가 많고 확률이 맞다는 것을 의미함

 

- 다진 분류를 이진분류로 치환해서 해결하는 방식

   1. one vs rest : multiclass 문제를 이진 분류로 치환해서 해결하는 방식, 시간이 많이 걸리지만 많이 사용됨

   2. one vs one : 작은 데이터를 다룰 때 사용. 전체 데이터가 아닌, 특정 데이터만 분류 모델을 만드는 것임

 

 

시그모이드 (Sigmoid Function)

 

 

import numpy as np

import matplotlib.pyplot as plt

 

 

 

def sigmoid (x):

    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)

y = sigmoid(x)

plt.plot(x,y,'g')

plt.plot([0,0],[1.0,0.0],':')

plt.title('Sigmoid Function')

plt.show()

 

 

 

 

 

▶ w(가중치)값에 따라 경사도 변함 

 

 

def sigmoid (x):

    return 1/(1+np.exp(-x))

x = np.arange(-5.0,5.0,0.1)

y1 = sigmoid(0.5*x)

y2 = sigmoid(x)

y3 = sigmoid(2*x)

plt.plot(x,y1,'r--',label='w:0.5')

plt.plot(x,y2,'g',label='w:1')

plt.plot(x,y3,'b--',label='w:2')

plt.plot([0,0],[1.0,0.0],':')

plt.title('Sigmoid Function')

plt.legend()

plt.show()

 

 

 

 

---

■ 분류모델의 평가지표

 

1. 혼동행렬(오분류표) : Confusion Matrix

 

: 분류 모델에 의한 분류 예측이 실제와 같은지 다른지를 표시하고 이를 평가하는 방법

※ 실제 상황에서 양성(1), 음성(0) / 예측 상황에서 양성(1), 음성(0)

 

 

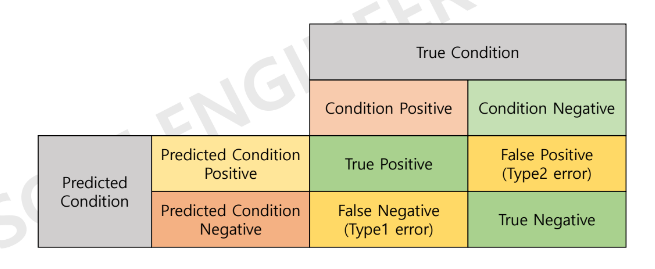
- positive / negative : 예측을 어떻게 했는지에 대한 예측값

- True / False : 예측이 실제와 같은지, 다른지 판단

 

True positive : 예측을 positive로 했는데 True임
False positive : 예측을 positive로 했는데 False임
True negative: 예측을 negative로 했는데 True임
False negative: 예측을 negative로 했는데 False임

 

- 혼동행렬 함수는 행을 true(실제), 열을 predict(예측) 값으로 이용
- 음성과 양성의 구분은 별도의 레이블을 지정하지 않으면 레이블 값의 정렬된 순서로 사용함
- (0과 1이며 0,1의 순서임(neg, pos) 0:Negative, 1:Positive)

    
            predict
        ----------------
            N  |  P
        ----------------
      |N|  TN  |  FP  |
  true|-|-------------|
      |p|  FN  |  TP  |
        ----------------

 

 

1) 정확도 (Accuracy)

  = TP+TN /전체 확률

 

2) 재현율 (민감도, Recall)

  : 실제 positive 상황에서 True여야 함 = 모델이 양성을 잘 찾아 냄

   = TP/TP+FN

 

3) 특이도

  : 아닌 상황에서 아니어야 함

   = TN/FP+TN

 

4) 정밀도 (Precision)

  : 예측을 positive로 했을 때 그중에서 True

  : 예측 상황이 분모로 들어가기 때문에 모델이 양성으로 예측한 것에 대한 신뢰도가 높음. 

   = TP/TP+FP

 

※ 재현율과 정밀도는 trade-off 관계 : 재현율이 높으면 정밀도는 낮아짐. 정밀도가 높으면 재현율이 낮아짐

    : 양성을 찾는데 굉장히 신중하다 = 잘 알려주지 않으려고 함 → 재현율 낮아짐

 

5) F1 score

   : F1 score 값이 높을 수록 좋음  

    = 2PR/(P+R) (Precision과 Recall의 조화 평균 값)

 

 

□  ROC curve 

 

 

 

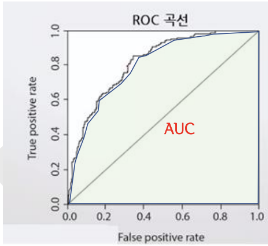
TPR : True Positive Rate = Recall
TNR : True Negative Rate = 특이도
FPR (거짓 양성률) = 1-특이도

 AUC : ROC curve 적분한 값. AUC가 클수록 좋음 (0.5이상이어야 함)

 

 

 

 

※  임계값(Cut-off value)  : 임계값보다 큰 경우 1로, 작은 경우 0으로 분류함. 즉, 분류 기준임

※  임계값을 어디에 두는 지가 재현율, 정밀도에 영향을 미침

 

- 임계값(threshold)이 높으면, 양성 확률이 적어짐.

- 확실한 증거가 존재하지 않는 한 양성으로 판단함. (매우 신중해짐)

- 반면에 낮으면, 양성이 많아지지만 실제로는 음성인, 거짓 양성이 많아짐.

 

 

2. 다중 클래스 혼동행렬

- Apple class의 경우

  

 

Apple Class metrics값

- TP = 7

- TN = (2+3+2+1) = 8

- FP = (8+9) = 17

- FN = (1+3) = 4

- Precision = 7/(7+17) = 0.29

- Recall = 7/(7+4) = 0.64

- F1-score = (2*0.29*0.64) / (0.29+0.64) = 0.399

 

 

□ Micro F1

: 마이크로 평균 F1-score라고 하며, 모델의 전체 TP, 전체 FP 및 전체 FN 을 고려하여 계산됨. 메트릭을 전역으로 계산하기 때문에 모든 측정값이 동일해짐 (Precision=Recall=Micro F1=Accuracy)

- Total TP = (7+2+1) =10

- Total FP = (8+9)+(1+3)+(3+2) =26

- Totla FN = (1+3)+(8+2)+(9+3) = 26

- Precision = 10/(10+26) =0.28

- Recall = 10/(10+26) 0.28

- Micro F1 = 0.28

 

 

□ Macro F1

 : 각 클래스에 대한 메트릭을 개별적으로 계산한 다음 측정값의 가중되지 않은 평균을 취함

 - Apple class F1-score = 0.40 

 - Orange class F1-score = 0.22 

 - Mango class F1-score = 0.11

 - Macro F1-score = (0.40+0.22+0.11)/3=0.24

 

□ Weighted F1

: 메크로 F1과는 달리 측정값의 가중 평균을 사용함. 각 클래스의 가중치는 해당 클래스의 총 샘플 수가 됨. 사과는 11개, 오렌지는 12개, 망고는 13개의 샘플을 사용하여 측정했기 때문에

- Weighted F1-score = {(0.40*11)+(0.22*12)+(0.11*13)} / (11+12+13) = 0.24